Return-Weighted Stress Tests
When we are looking at stress tests, we are, by definition, interested in extreme returns. Our standard predictive stress tests are based on betas estimated from two years of backcast returns, equally weighted. When it comes to stress tests, there is a good case to be made for this equally-weighted approach. However, it is possible that the beta of some securities will be meaningfully different in extreme markets than in calm markets.
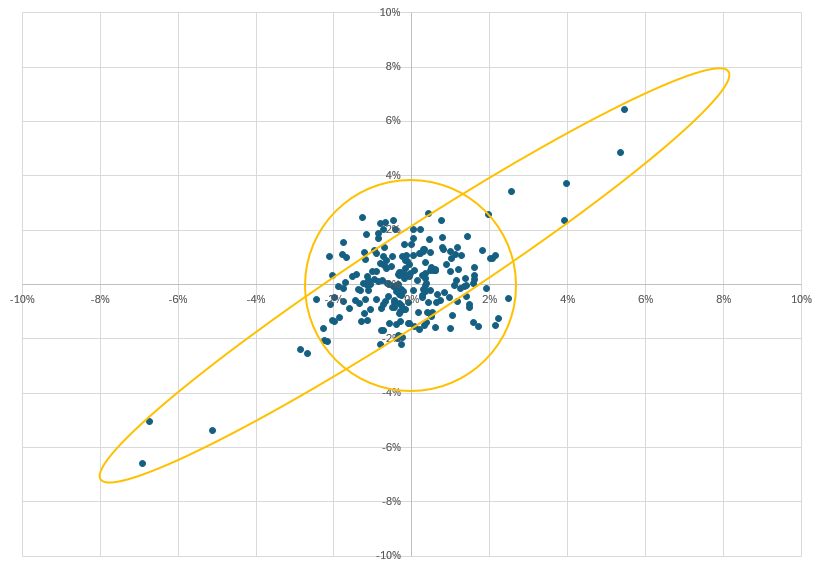
Paul Wilmott has described a possible “rings of Saturn” pattern, where, when we graph the returns of a security against an index, most of the points form a circular blob near the origin, while a few extreme points form a notably tilted ellipse. The blob has a very low beta, compared to the ellipse. Because there are far more points in the blob, the overall beta is much closer to the beta of the blob than the ellipse.
If this is the case, then when calculating our beta, rather than equally weighting the returns, we might want to put more weight on the more extreme points. The advantage of this return- or risk-weighted approach to calculating betas is that it is putting more weight on the extreme scenarios that we are most interested in. The downside is that there are very few extreme points, which renders any statistics that rely heavily on these extreme points less certain and less stable.
In our stress test calculations, the return-weighted betas are calculated using a weighted least squares regression, where the weights are based on the sum of the squared returns of the factors that define the scenario.
For more on stress tests, see our paper, Stress Tests and Correlation.